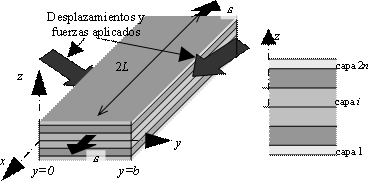
Se considera un multicapa elástico (q1,...,qn)5 compuesto de N = 2n capas de materiales ortotrópicos. La dirección de las z es una dirección de ortotropía para todas las capas (véase la Figura 1). El multicapa tiene una longitud de 2L, un ancho de b y un espesor total de 2e. El multicapa se somete a (véase la Figura 1)
Figura 1. Multicapa simétrico.
Suponemos que la longitud
2L del multicapa es mucho más grande que las otras dimensiones
del multicapa. De esta manera, se puede suponer que los esfuerzos y deformaciones
son independientes de x lo suficientemente lejos de los bordes ![]() [1].
El problema se vuelve bidimensional.
[1].
El problema se vuelve bidimensional.
Con el fin de evaluar los esfuerzos y los desplazamientos, el programa utiliza el modelo multipartícula M4-5N. El multicapa (objeto 3D) se vuelve una superposición de N = 2n placas de Reissner [2] (un objeto 2D con N partículas materiales en cada punto geométrico y para cada partícula, se consideran 5 campos cinemáticos) acoplados por esfuerzos de interface. Este modelo es similar al modelo local de Pagano [3] y ya se validó para los problemas termo-elásticos [1, 4, 5]. La aplicación del modelo en nuestro problema nos permite simplificar el problema de manera que se obtiene un problema unidimensional en y [1].
Se obtiene el modelo mediante una adaptación de la formulación clásica de Hellinger-Reisner para problemas elásticos 3D [6] y una aproximación pertinente del campo de esfuerzos. En cada capa, se seleccionan esfuerzos sab(donde a, b = x, y) de tipo polinomial en z de grado 1. La utilización del equilibrio 3D da, para los esfuerzos fuera del plano sax y sxx, aproximaciones polinomiales en z (en cada capa) de grados 2 y 3, respectivamente. Los coeficientes de estos polinomios son los esfuerzos generalizados (campos en y) siguientes:
|
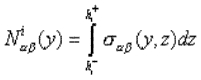 |
(1) |
|
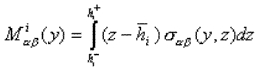 |
(2) |
|
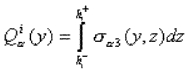 |
(3) |
|
(4) | |
|
(5) |
donde ![]() es
la altura de la piel superior de la capa i,
es
la altura de la piel superior de la capa i,![]() es la altura de la piel inferior de la capa i,
es la altura de la piel inferior de la capa i, ![]() es
la altura promedio de la capa i, y a,
b =
x, y. Los esfuerzos de interface definidos anteriormente tienen
un significado físico ya que representan el valor de los esfuerzos
fuera del plano calculados en las interfaces de las capas. Al ingresar los
esfuerzos 3D aproximados en la funcional de Hellinger-Reissner se identifican
los 5N (N = 2n, número total de capas) desplazamientos
generalizados siguientes:
es
la altura promedio de la capa i, y a,
b =
x, y. Los esfuerzos de interface definidos anteriormente tienen
un significado físico ya que representan el valor de los esfuerzos
fuera del plano calculados en las interfaces de las capas. Al ingresar los
esfuerzos 3D aproximados en la funcional de Hellinger-Reissner se identifican
los 5N (N = 2n, número total de capas) desplazamientos
generalizados siguientes:
|
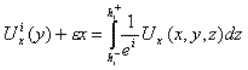 |
(1) |
|
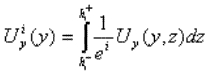 |
(2) |
|
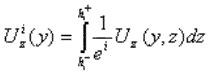 |
(3) |
|
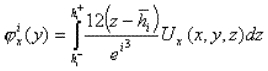 |
(4) |
|
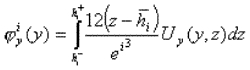 |
(5) |
donde Ux, Uy y Uz son los desplazamientos 3D. Cabe destacar el hecho de que nuestros campos generalizados dependen únicamente de y.
Enseguida, la estacionalidad de la funcional de Hellinger-Reissner con respecto a los esfuerzos generalizados da las ecuaciones generalizadas de comportamiento. Por otra parte, la estacionalidad de la funcional con respecto a los desplazamientos generalizados da las ecuaciones de equilibrio y condiciones generalizadas de frontera (condiciones en los bordes). Puesto que se trata de ecuaciones con y, nuestro problema es unidimensional en y.
Encontraremos en [5] la construcción detallada de este modelo, que además, se puede aplicar a cualquier problema mecánico de multicapas.
Para resolver las ecuaciones, se simplifica primero el problema con la ayuda de las simetrías con respecto al plano z = 0. Así, la geometría del problema se reduce a la de la Figura 2.
Figura 2. Problema simplificado.
Después, por operaciones matriciales el problema se reduce a la solución de un sistema diferencial de segundo orden:
| (11) |
donde k es un vector cuyas componentes se deducen de los esfuerzos y desplazamientos generalizados, F es una matriz constante y Yin es un vector constante cuyas componentes se deducen de las deformaciones inelásticas debidas a la carga higrotérmica. Esta ecuación diferencial (11) se resuelve mediante una formulación variacional y un mallado del intervalo[0,b] . La formulación variacional se obtiene de manera similar a la de [1]. El problema variacional se reduce finalmente a la solución de un sistema de ecuaciones lineales del tipo:
| (12) |
donde R es la matriz de rigidez (se conocen sus coeficientes), c es un vector desconocido cuyas componentes son los valores en los nodos (del mallado del intervalo [0,b]) de las componentes del vector k , c es un vector conocido cuyas componentes se deducen de las cargas. Así, podemos determinar los valores de los esfuerzos y desplazamientos generalizados en los nodos del mallado y sobretodo, podemos calcular el efecto de borde sobre los esfuerzos de interface.
Muchos cálculos [1] han comprobado que los resultados convergen con rapidez (con un número de nodos razonable) y que no existen singularidades. Los cálculos también se validaron al comparar los resultados con las soluciones obtenidas en la bibliografía y con resultados de elementos finitos 3D.
Observaciones importantes
|
En DEILAM, los esfuerzos cortantes en las interfaces entre las capas no verifican la condición de frontera 3D: tyz = 0 Para que verifiquen esta condición deberíamos enriquecer el modelo M4-5N. Sin embargo, aún si no se verifica la condición en los límites 3D, el M4-5N hace una buena descripción del esfuerzo cortante en el ancho [0,b] [1, 3]. Los elementos finitos 3D cerca de los bordes y de las interfaces (entre capas de materiales diferentes) dan resultados que dependen del mallado (existen singularidades). DEILAM da valores finitos en las interfaces y los resultados convergen rápidamente. Para ciertos materiales, estos valores finitos probaron ser capaces de pronosticar el inicio de la delaminación [7], [8], [9] |
Referencias
[1] DIAZ DIAZ A, CARON JF, CARREIRA RP, “Software application for evaluating interfacial stresses in inelastic symmetrical laminates with free edges”, Journal of Composite Structures, 58, 195-208, 2002
[2] REISSNER E, “The effect of transverse shear deformation on the bending of elastic plates”, Journal of Applied Mechanics, A, 69-77, 1945.
[3] PAGANO NJ, PIPES RB, “The influence of stacking sequence on laminate strength”. Journal of Composite Materials, Vol. 5, p.50, 1971.
[4] CARREIRA RP, CARON JF, DIAZ DIAZ A. “Model of multi-layered materials for interface stresses estimation and validation by finite element calculations”, Mechanics of Materials, 34, 217-230, 2002.
[5] DIAZ DIAZ A, CARON JF, CARREIRA RP. “Un modèle de stratifiés”. Comptes Rendus de l'Académie des Sciences, 329, 873-879 (2001).
[6] REISSNER E, “On a variational theorem in elasticity”, Journal of Mathematics and Physics, 29, 90-95, 1950.
[7] CARON JF, CARREIRA RP, DIAZ DIAZ A. “Critère d’initiation de délaminage dans les stratifiés”. Comptes Rendus de l’Académie des Sciences, 327, 1291-1296 (1999).
[8] CARON JF, DIAZ DIAZ A, CARREIRA RP, CHABOT A, EHRLACHER A. “Multi-particle modelling for the prediction of delamination in multi-layered materials”. Artículo aceptado para publicación en la revista Composite Science and Technology, 2005.
[9] DIAZ DIAZ A, CARON JF. “Prediction of the onset of mode III delamination in carbon-epoxy laminates”. Artículo aceptado para publicación en la revista Composite Structures, 2005.