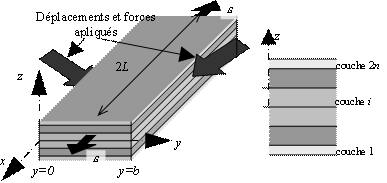
On considère un multicouche élastique (q1,...,qn)5 composé de N=2n couches de matériaux orthotropes. La direction des z est une direction d’orthotropie pour toutes les couches (voir Figure 1). Le multicouche a une longueur 2L, une largeur b et une épaisseur totale 2e. Le multicouche est soumis à (voir Figure 1).
Figure 1. Multicouche symétrique.
Nous supposons que la longueur
2L du multicouche est beaucoup plus grande que les autres dimensions
du multicouche. De cette sorte, on peut supposer que les contraintes et les
déformations son indépendantes de x suffisamment loin des
bords 
[1].
Le problème devient ainsi bidimensionnel.
Pour évaluer les contraintes et les déplacements, le logiciel utilise le modèle multiparticulaire M4-5N. Le multicouche (objet 3D) devient une superposition de N=2n plaques de Reissner [2] (un objet 2D avec N particules matérielles dans chaque point géométrique et pour chaque particule, 5 champs cinématiques sont considérés) couplés par des efforts d’interface. Ce modèle est similaire au modèle local de Pagano [3] et a déjà été validé pour des problèmes thermo-élastiques [1,4,5]. L’application du modèle à notre problème nous permet de simplifier le problème de sorte qu’on obtient un problème monodimensionnel en y [1].
Le modèle est obtenu moyennant une adaptation de la formulation classique d’Hellinger-Reissner pour des problèmes élastiques 3D [6] et une approximation pertinente du champ de contraintes. Dans chaque couche, on choisit des contraintes sab(où a, b = x, y) polynomiales en z de degré 1. L’utilisation de l’équilibre 3D donne pour les contraintes hors plan saz et szz des approximations polynomiales en z (dans chaque couche) de degrés 2 et 3, respectivement. Les coefficients de ces polynômes sont les efforts généralisés (des champs en y) suivants:
|
 |
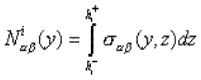(1) |
|
 |
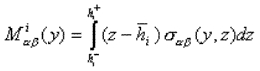(2) |
|
 |
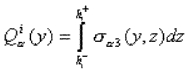(3) |
|
 |
(4) |
|
 |
(5) |
où
est la cote
de la peau supérieure de la couche i, 
est la cote de la peau inférieure de la couche i, 
est
la cote moyenne de la couche i, et a, b
= x, y. Les efforts d’interface définis précédemment
ont bien une signification physique puisqu’ils représentent la
valeur des contraintes hors plan calculées aux interfaces entre les
couches. En injectant les contraintes 3D approchées dans la fonctionnelle
d’Hellinger-Reissner on identifie les 5N (N=2n,
nombre total de couches) déplacements généralisés
suivants:
|
 |
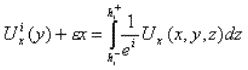(1) |
|
 |
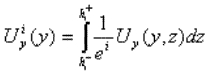(2) |
|
 |
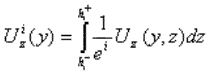(3) |
|
 |
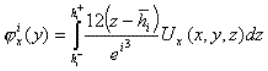(4) |
|
 |
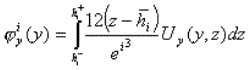(5) |
où Ux, Uy et Uz sont les déplacements 3D. Soulignons le fait que nos champs généralisés dépendent uniquement dépendent uniquement de y.
Ensuite, la stationnarité de la fonctionnelle d’Hellinger-Reissner par rapport aux efforts généralisés donne les équations de comportement généralisées. D’autre part, la stationnarité de la fonctionnelle par rapport aux déplacements généralisés donne les équations d’équilibre et les conditions aux bords généralisées. Puisqu’il s’agit d’équations en y, notre problème est monodimensionnel en y.
Nous trouverons dans [5] la construction détaillée de ce modèle, qui en outre, peut être appliqué à n’importe quel problème mécanique des multicouches.
Pour résoudre les équations, on simplifie d’abord le problème à l’aide des symétries par rapport au plan z = 0. De cette sorte la géométrie du problème se réduit à celle de la Figure 2.
Figure 2. Problème simplifié
Puis, par des opérations matricielles on réduit le problème à la résolution d’un système différentiel du second ordre:
 |
(11) |
où k est un vecteur dont les composantes se déduisent des efforts et des déplacements généralisés, F est une matrice constante et Yin est un vecteur constant dont les composantes se déduisent des déformations anélastiques dues au chargement hygrothermique. Cette équation différentielle (11) est résolue moyennant une formulation variationnelle et un maillage de l’intervalle [0,b] . La formulation variationnelle est obtenue d’une façon similaire à celle dans [1]. Le problème variationnel se réduit finalement à la résolution d’un système d’équations linéaires du type :
 |
(12) |
où R est la matrice de rigidité (ses coefficients sont connus), est un vecteur inconnu dont ses composantes sont les valeurs aux nœuds (du maillage de l’intervalle [0,b]) des composantes du vecteur k , c est un vecteur connu dont ses composantes sont déduites des chargements. Nous pouvons ainsi déterminer les valeurs des efforts et des déplacements généralisés aux nœuds du maillage et surtout, nous pouvons calculer l’effet de bord sur les efforts d’interface.
Plusieurs calculs [1] ont prouvé que les résultats convergent rapidement (avec un nombre de nœuds raisonnable) et qu’il n’existe pas de singularités. Les calculs ont aussi été validés en comparant les résultats avec des solutions cueillies dans la littérature et avec des résultats d’éléments finis 3D.
Remarques importantes
|
Les efforts de cisaillement aux interfaces entre les couches de DEILAM ne vérifient pas la condition aux limites 3D : tyz = 0 Pour qu’ils vérifient cette condition nous devrions enrichir le modèle M4-5N. Cependant, même si la condition aux limites 3D n’est pas vérifiée, le M4-5N fait une bonne description du cisaillement sur la largeur [1]. Les éléments finis 3D près des bords et des interfaces (entre des couches de matériaux différents) donnent des résultats qui dépendent du maillage (il existe des singularités). DEILAM donne des valeurs finies aux interfaces et les résultats convergent rapidement. Pour certains matériaux, ces valeurs finies ont déjà prouvé être capables de prédire l’initiation du délaminage [7], [8], [9] |
Références
[1] DIAZ DIAZ A, CARON JF, CARREIRA RP, “Software application for evaluating interfacial stresses in inelastic symmetrical laminates with free edges”, Journal of Composite Structures, 58, 195-208, 2002
[2] REISSNER E, “The effect of transverse shear deformation on the bending of elastic plates”, Journal of Applied Mechanics, A, 69-77, 1945.
[3] PAGANO NJ, PIPES RB, “The influence of stacking sequence on laminate strength”. Journal of Composite Materials, Vol. 5, p.50, 1971.
[4] CARREIRA RP, CARON JF, DIAZ DIAZ A. “Model of multi-layered materials for interface stresses estimation and validation by finite element calculations”, Mechanics of Materials, 34, 217-230, 2002.
[5] DIAZ DIAZ A, CARON JF, CARREIRA RP. “Un modèle de stratifiés”. Comptes Rendus de l'Académie des Sciences, 329, 873-879 (2001).
[6] REISSNER E, “On a variational theorem in elasticity”, Journal of Mathematics and Physics, 29, 90-95, 1950.
[7] CARON JF, CARREIRA RP, DIAZ DIAZ A. “Critère d’initiation de délaminage dans les stratifiés”. Comptes Rendus de l’Académie des Sciences, 327, 1291-1296 (1999).
[8] CARON JF, DIAZ DIAZ A, CARREIRA RP, CHABOT A, EHRLACHER A. “Multi-particle modelling for the prediction of delamination in multi-layered materials”. Article accepté pour publication dans la revue Composite Science and Technology, 2005.
[9] DIAZ DIAZ A, CARON JF. “Prediction of the onset of mode III delamination in carbon-epoxy laminates”. Article accepté pour publication dans la revue Composite Structures, 2005.
