Calculations of this module are based essentially on the classical model for multi-layeredplates [1]. For a multi-layered material defined by the user, the module is able to carry out three kinds of calculations.

1. STIFFNESSES calculation. This type of calculation makes possible to determine global properties of the multi-layered material, such as the ABBD matrix, apparent thermal expansion coefficients, apparent Young’s moduli... [1]
2. STRESSES calculations. For a given hygro-thermo-mechanical load the software calculates the stresses and strains in the layers, and this is done in the global or local coordinates system (the orthotropy directions in each layer).
3. STRENGTHS calculations. For a given proportional load, the software determines the load level for which the first ply failure (FPF) occurs. Moreover, the software makes possible to visualize the intersection of a 2D plane with the failure envelope (an hypersurface) by making use of the FPF criterion .

It is possible to select the calculation type in the main window of the module LAMINATES (see Figure 8). All of the calculations may take into account hygrothermal loads (moisture and temperature). This may be activated by clicking on <<Calculation and report options>> in the menu bar of the main window in the module.

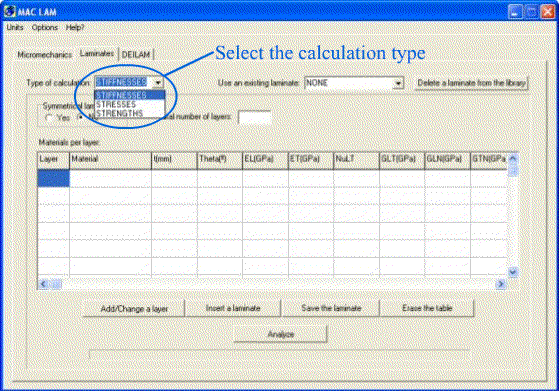
Figure 8. Selection of calculation type in LAMINATES module

In order to define a laminate, the user first has to tell if the laminate is symmetrical or not and enter the total number of layers (see Figure 9; for a symmetrical multi-layered material, the total number of layers must be a even number).

Figure 9. Definition of the multi-layered material symmetry and the total number of layers.

In the module LAMINATES, the properties which have to be defined for each layer are:

• Name of the material of which the layer is made
• Thickness of the material of which the layer is made in mm or min (mili-inches)
• Angle q (Theta) in degrees (it is an angle in the orthotropy direction L with respect to the global x-axis of the laminate, see Figure 10).

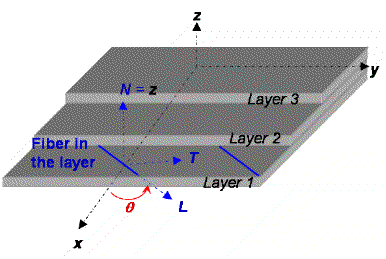
Figure 10. Global (x, y, z) and local (L, T, N) directions

• Elastic properties in the orthotropy directions ( L, T, N )
  • Young’s moduli _L and E_T in GPa or in MPsi.
  • Shear moduli G_LT, G_LN, G_TN in GPa or in MPsi. It is necessary to enter the last two shear modulii in order to determine the out-of-plane stiffnesses of the laminate.
  • Poisson’s ratio n_LT .
• Thermal expansion coefficients a_L, a_T and a_LT in the other orthotropy directions ( L, T, N ). Their units are (°C)^-1 or(°F)^-1. These data are necessary only in case you decide to take into account the thermal strains.
• Hygroscopic coefficients b_L, b_T and b_LT . These data are necessary only in case you decide to take into account the humidity absorption.
• Failure criterion and criterion data (necessary only for calculating STRENGTHS). Three kinds of criteria may be considered:
  1. The Tsai-Hill criterion. In the column <<Criterion>> you have to type 1. The data you have to enter for this kind of criterion are:
     • X_t (X_t > 0), the tensile strength in the fibers direction (L), in MPa or in KPsi
     • Y_t (Y_t > 0), the tensile strength in the transverse direction (T), in MPa or in KPsi
     • S (S > 0), the longitudinal-transverse shear strength, in MPa or in KPsi
  2. The Hoffman criterion. In the column <<Criterion>> you have to type 2. The data you have to enter for this kind of criterion are:
     • X_t (X_t > 0), the tensile strength in the fibers direction, (L) in MPa or in KPsi
     • X_c (X_c > 0), the compressive strength in the fibers direction, (L) in MPa or in KPsi
     • Y_t (Y_t > 0), the tensile strength in the transverse direction (T), in MPa or in KPsi
     • Y_c (Y_c > 0), the compressive strength in the transverse direction (T), in MPa or in Kpsi
     • S (S > 0), the longitudinal-transverse shear strength, in MPa or in KPsi
  3. The Tsai-Wu criterion. In the column <<Criterion>> you have to type 3. The data that you should enter for this kind of criterion are the same as for the Hoffman criterion, but you also have to enter the coefficient value F₁₂ which appears in the criterion. The F₁₂ units are (MPa)^-2 or (KPsi)^-2.

In order to enter the above-said layers properties, the user may proceed in several ways. It is worth underlining that this task may be done quickly thanks to the libraries used by MAC LAM

References
[1] R.M. Jones, "Mechanics of composite materials", second edition, Taylor & Francis, United States, 1999.